ফিবুনাচি না বিরহাঙ্ক- শেষ পর্ব

(গতকালের পর)

এবার আমি বিরহাঙ্ক-ফিবুনাচি রাশির আরও অনেক প্রয়োগশীলতা বিষয়ে পাঠককে নিয়ে চলে যাব প্রকৃতির একটি গোপন প্রকোষ্ঠে। কিন্তু তার আগে, পেশাদার গাণিতিক হিসেবে, সংস্কৃত-প্রাকৃত-বাংলা কাব্যের ছন্দশাস্ত্রের সঙ্গে গণিতের যে আরও কটি শাখার চমকপ্রদ সম্পর্ক আছে, তার সামান্য আভাস দেওয়ার লোভ সংবরণ করতে পারছি না। অঙ্কের রানি গণিতের একটি প্রাচীন শাখার নাম সংখ্যাতত্ত্ব ( theory of Numbers)। সংখ্যা বলতে এখানে কেবল প্রাকৃতিক সংখ্যাই বোঝাচ্ছে... ১, ২, ৩, ৪, ...। তত্ত্বটির মূল বিষয়বস্তুই হলো এই প্রাকৃতিক সংখ্যাগুলো, বিশেষ করে যাদের বলা হয় মৌলিক সংখ্যা। অর্থাৎ যে সব সংখ্যা এমনই স্বাধীনচেতা যে একমাত্র ১ আর তারা নিজেরা ছাড়া অন্য কোনো সংখ্যা দিয়ে তাদের ভাগ করা যাবে না। আপনি জোর করে চেষ্টা করতে পারেন, তবে একটা অবশিষ্ট থেকেই যাবে। উদাহরণ: ২, ৩, ৫, ৭, ১১, ১৩, ...। এদের নিয়ে গল্প বলতে শুরু করলে দিন ফুরিয়ে রাত হবে, রাত ফুরিয়ে আবার হবে দিন, তবুও আরব্য উপন্যাসের গল্পের মতো গল্প কখনোই ফুরাবে না। অনভিজ্ঞ পাঠক হয়তো কপাল কুঁচকে বলবেন, এ আবার কেমন কথা। হাতে গুণেই তো বলা যায় একের পর এক মৌলিক সংখ্যাগুলো ১৭, ১৯, ২৩, ২৯, ৩১, ...। আপনি নিজেকে বাহবা দিতে শুরু করেছেন, হয়তো বা এই ভেবে যে, ‘মূর্খ গাণিতিক’রা যেখানে দিনের পর দিন আর রাতের পর রাত কাটিয়ে দেয় যার গল্প বলতে, সে বিষয়টি আপনি আনাড়ি মানুষ হয়েও গড়গড় করে আওড়ে যেতে পারছেন। আপনি অতিশয় তীক্ষ্ণ মেধার মানুষ তাতে হয়তো সন্দেহ নেই, কিন্তু আপনাকে যদি জিজ্ঞেস করা হয়, এই আপাতসহজ সংখ্যাগুলো যখন ১০০-র ওপরে চলে যায় তখনো কি এত সহজে বলতে পারবেন কোনটা মৌলিক, কোনটা মৌলিক নয়? বড় কথা আপনি কি নিশ্চিতভাবে বলতে পারবেন এই মৌলিক সংখ্যাগুলো শেষ পর্যন্ত একটা জায়গায় গিয়ে থেমে যায়, না তারা অনন্তকাল ধরে চলতে থাকে? না, পারবেন না। বড় বড় গাণিতিকদের মাথা ঘেমে গিয়েছিল এ প্রশ্নের জবাব দিতে। তিন-চারজন ভদ্রলোক শেষে এ প্রশ্নের চূড়ান্ত সমাধান পেয়েছিলেন বটে এবং পাওয়ার ফলে তাঁরা গণিত জগতে বিস্তর যশ-খ্যাতি অর্জন করে গেছেন। তাঁদের আবিষ্কৃত তথ্য অনুযায়ী মৌলিক সংখ্যা সীমাহীন। তবে যতই ওপরের দিকে উঠতে থাকেন তাঁরা, ততই তাদের পারস্পরিক দূরত্ব বৃদ্ধি পেতে থাকে।

অনেকটা পাহাড়ের গা বেয়ে ওপরে ওঠার সময় যেমন বায়ুর ঘনত্ব ক্রমশ কমতে থাকার ফলে বায়ুচাপও কেবলই নিম্নমুখী হতে থাকে। কৌতূহলী গণিতবিদদের জন্য অত্যন্ত আকর্ষণীয় ও গভীর চিন্তাভাবনার বিষয় ছিল যে, ঠিক আছে, তারা দূরে দূরে থাকে, কিন্তু কারও যদি একটা বড়সড় মৌলিক সংখ্যা দরকার পড়ে (যেমন বর্তমান যুগের নিরাপত্তা ব্যবসায়ী, ব্যাংক কর্তৃপক্ষ ও সরকারি-বেসরকারি কোষাগার রক্ষকরা) তাহলে তারা কোথায় খুঁজবে সেই সংখ্যাগুলো? তাছাড়া, বাস্তব জীবনের প্রয়োজনীয়তার কথা বাদ দিলেও একটা গাণিতিক কৌতূহল থেকেই যায়। তাইতো, এরা কোথায় থাকে, এদের ঠিকানা কী? পাঠক হয়তো বিশ্বাসই করতে চাইবেন না যে, এ প্রশ্নের উত্তর তো এখনো কেউ আবিষ্কার করতেই পারেনি, অদূর ভবিষ্যতেও কেউ পারবে কি না, সন্দেহ-এতই অবিশ্বাস্য রকম শক্ত এই প্রশ্নটি। তবে ১৮৫৯ সালে জার্মানির বার্নার্ড রিম্যান নামের ৩৩ বছর বয়স্ক এক যুবক, ইতিহাসে যিনি চিরস্মরণীয় হয়ে থাকবেন এবং যাঁর অকালমৃত্যু হয়েছিল মাত্র ৪০ বছর বয়সে, এ বিষয়ে অনেক গভীর গবেষণা করে গেছেন। তিনি এর পূর্ণ সমাধান লাভ করতে সক্ষম হননি বটে, তবে একটা আন্দাজ রেখে গিয়েছিলেন ভবিষ্যতের গাণিতিক প্রজন্মের জন্য।

যেটাকে বলা হয় ‘রিম্যান কঞ্জেকচার’। কঞ্জেকচার বলতে বোঝায় একটা সম্ভাব্য ফলাফল। যা শুধু অনুমান করে বলা গুটিকয় সাক্ষ্যপ্রমাণের ভিত্তিতে, কিন্তু যার ত্রুটিহীন প্রামাণিক সত্যতা এখনো অপ্রতিষ্ঠিত। গণিতের গবেষণা ক্ষেত্রে এর চেয়ে ‘দাঁত-বসানো-দায়’ সমস্যা আর দ্বিতীয়টি নেই। এই কঞ্জেকচারের সমাধান যে দিতে পারবে, সে চিরজীবী হয়ে থাকবে, এটা এ করকম গ্যারান্টেড। এই বিশাল সাগর পাড়ি দেওয়ার চেষ্টা করতে গিয়ে কত বড় বড় নাবিক (মানে গণিতসায়রের নাবিক) যে দিশা হারিয়ে ভরাডুবি খেয়েছেন, তার সীমা নেই। মজার ব্যাপার কী জানেন? একটা বড় স্বপ্নকে লক্ষ্য করে যখন একজন দুঃসাহসী মেধাবী যাত্রী চলতে শুরু করেন কোনো দুর্গম অজানা পথের ওপর দিয়ে, তখন শেষ গন্তব্যে পৌঁছুতে সক্ষম না হলেও পথিমধ্যেই এমন সব চমকপ্রদ দৃশ্যের অস্তিত্ব ধরা দেয়, তার কাছে যে সেই তথ্যগুলিও পৃথিবীকে আগের চেয়ে অনেকটাই সমৃদ্ধ করে যায়। রিম্যান কঞ্জেকচার প্রমাণ করবার চেষ্টা করতে আজ পর্যন্ত কেউই পুরোপুরি সফল হননি, কিন্তু সেই চেষ্টা থেকেই বেরিয়ে এসেছে গণিতের আরও কত বিচিত্র রহস্য।

কত রং, কত বর্ণশোভাতে দীপ্যমান কত নব নব কুঞ্জকানন আবিষ্কৃত হয়ে গণিতকে করেছে রূপবান, ধনাঢ্য, বর্ণাঢ্য। তাই বলি, একটা বড় ব্যর্থতাও অনেক সময় অনেক গুপ্তধনের সন্ধান দেয়। রিম্যান কঞ্জেকচার ও তার আনুষঙ্গিক বিষয়াদি নিয়ে কৌতূহলী পাঠক যদি কোনো সহজপাঠ্য বই পড়তে চান তাহলে আমি তাকে মার্কাস ডু সটয়ের অসাধারণ গ্রন্থ The Music of the Primes (published by Harper Collins Publishers, 2003; first paperback Perennial edition published in 2004) সংগ্রহ করার চেষ্টা করতে বলব। মূলত গণিতের বই হলেও এটা রহস্য উপন্যাসের মতোই মনে হবে পড়বার সময়। একবার পড়তে শুরু করলে শেষ না করে ওঠা শক্ত। যা-ই হোক, আমার আজকের প্রসঙ্গ এতটা উচ্চাভিলাষী নয়। রীতিমতো সাদামাটাই বলতে পারেন তুলনামূলকভাবে। সংখ্যা গণিতের আরেকটি শাখার নাম হলো Partition Theory. না, দেশ ভাগাভাগি নয়, সম্পত্তি ভাগাভাগিও নয়। পূর্ণ সংখ্যার ভাগাভাগি। একটা প্রাকৃতিক বা পূর্ণ সংখ্যাকে নিম্নতর সংখ্যাগুলো দিয়ে কতভাবে ভাগ করা যায়, গোড়ার প্রশ্নটা হলো এই। বাস্তব জগতের প্রয়োগশীলতা নিয়ে অতিরিক্ত উদ্বিগ্ন যাঁরা, তারা হয়তো বলবেন, এমন একটা নীরস জিনিস নিয়ে অনর্থক সময় নষ্ট করার দরকারটা কী? দরকার আছে বইকি। আপনি যদি কোনো ক্যাসিনোতে যান কখনো জুয়ার চাকায় নিজের ভাগ্য পরীক্ষা করার জন্য, তাহলে এই সংখ্যা ভাগাভাগির ব্যাপারটি একটু আয়ত্ত করে গেলে উপকার হতে পারে। কারণ সেখানে ‘সম্ভাবনা’ বা প্রভাবিলিটি গণনার ক্ষমতা কার কত, তার ওপরই নির্ভর করে খেলোয়াড়ের জুয়ার ভাগ্য। এই গণনার পেছনে রয়েছে এই সংখ্যা-বিভক্তির সমস্যাটি। তাছাড়া ব্যবহারিক প্রয়োগ বাদ দিলেও কৌতূহলী মনের একটা স্বাভাবিক তাড়না তো আছেই। এই তাড়না থেকেই তো জন্ম নিয়েছে পৃথিবীর কত না অমর সৃষ্টি। উদহারণ হিসেবে ধরা যাক ৬ সংখ্যাটি। অন্য যেকোনো ছোটখাট সংখ্যা হলেও চলত, তবে ৬ সংখ্যাটিকে বাছাই করার উদ্দেশ্য জুয়াড়ির গুটিতে সাধারণত ১ থেকে ৬ পর্যন্ত সংখ্যাগুলোই থাকে। ৬ এর নিচে মোট পাঁচটি পূর্ণ সংখ্যা ১, ২, ৩, ৪, ৫। প্রশ্ন হলো, এই পাঁচটি সংখ্যা ‘কতভাবে’ ব্যবহার করে তাদের যোগফল ৬ পাওয়া যাবে? এই যে ‘কতভাবে’ প্রশ্নটি, তাকেই বলা হয় পার্টিশন বা বিভক্তি। সজাগ পাঠক হয়তো তৎক্ষণাৎ প্রশ্ন তুলবেন, সংখ্যাগুলো কীভাবে ব্যবহার করা হবে তার কোনো নিয়মকানুন নেই? অবশ্যই আছে এবং একেক নিয়ম অনুযায়ী আমরা একেক ফল পাব। যেমন, যদি বলা হয় কোনো সংখ্যা দুবার ব্যবহার করা যাবে না এবং দুটি বা তিনটি সংখ্যা আগে-পরে ব্যবহার করার পর সেগুলোকে ওলটপালট করে লিখলে কোনো ভিন্ন সংখ্যা ধরা হবে না।

তাহলে হিসাবটা হবে এ রকম: ৬=১+২+৩=২+৪=১+৫ অর্থাৎ মোটমাট ৩টি। ৬=১+১+৪=২+২+২=৩+৩ এগুলো নিষিদ্ধ এবং ২+৪ একবার গোনা হলে ৪+২ কে ভিন্ন বিভাগ ধরা যাবে না। অতএব এই হিসাব অনুযায়ী ৬ এর বিভক্তি সংখ্যা হলো ৩। এবার ধরুন, ওপরের নিয়মটি একটু শিথিল করে বলা হলো: সংখ্যাগুলো আলাদাই থাকবে, তবে তাদের বিন্যাস অর্থাৎ কোনটা আগে কোনটা পরে সেটা পরিবর্তন করা হলে বিভক্তিটাও সম্পূর্ণ ভিন্ন হয়ে যাবে। তাহলে মোট কটা বিভক্তি পেতে পারি আমরা? নিচে তার পুরো তালিকাটিই দিয়ে দিলাম: ৬=২+৪=৪+২=১+৫=৫+১=১+২+৩=১+৩+২=২+৩+১=২+১+৩=৩+১+২=৩+২+১; মোট কটা হলো? হাতে গুনেই পাবেন ১০টা। ৩ থেকে এক লাফে চলে গেল ১০-এ তে! এখন আরেকটি নিয়ম আরোপ করা হবে ৬-এর বিভক্তির ওপর: কেবল ১ আর ২, এ দুটি সংখ্যাই ব্যবহার করার অনুমতি আছে, তবে তাদের ভিন্ন বিন্যাসকে ভিন্ন বিভক্তি বলেই গণ্য করা হবে। শুধু তা-ই নয়, ১ আর ২ এর ব্যবহার যতবার ইচ্ছা ততবারই করা যাবে এবং প্রতিবারই তাতে একটা নতুন বিভক্তি পাওয়া যাবে। ভীষণ অবাস্তব বলে মনে হচ্ছে বুঝি? তাহলে একটা ‘বাস্তব’ উদাহরণ দেওয়া যাক, ধরুন একটি শিল্পমনা মেয়ের খুব ফুলের সখ, অথচ ফ্ল্যাটবাসী হওয়ার ফলে বাইরের বাগানে গাছ লাগানোর উপায় নেই তার। অতএব ফুলের পটে গাছ লাগিয়ে দুধের স্বাদ ঘোলে মেটানো ছাড়া বেচারার শখ মেটানোর অন্য কোনো পথ নেই। সে বাজার থেকে ৬টি পট কিনে নিয়ে এল, সঙ্গে ৬টি ফুলের চারা। ঘরে এনে খুব খাটাখুটি করে পটগুলোর গায়ে আলপনা এঁকে বেশ আকর্ষণীয় করে তুলল। এখন তার মনে প্রশ্ন: কোন পটে কোন চারাগুলো লাগাবে। একটা পটে সে ১টা বা বড়জোর ২টা চারা লাগাতে প্রস্তুত, কিন্তু তার বেশি নয়। যেহেতু পটগুলোতে আলপনা আঁকা, সেহেতু ১ নম্বর পটে ১ নম্বর চারা ও ২ নম্বর পটে ২ নম্বর চারা, আর ১ নম্বর পটে ২ নম্বর চারা ও ২ নম্বর পটে ১ নম্বর চারা ঠিক একই বিভক্তি নয়। কথা হলো, এই নিয়ম অনুসারে মোট কতগুলো বিভক্তি সম্ভব যাতে তার রুচির খেলাপ না হয়? প্রশ্নটা পাঠকের কাছে যত সহজ মনে হচ্ছে আসলে হয়তো ততটা সহজ নয়। সুতরাং পাঠকের সুবিধার জন্য আমরা প্রথমেই ৬-তে না গিয়ে ১ থেকে শুরু করব। ১: ১=১ বিভক্তি সংখ্যা= ১ ২: ২=১+১ বিভক্তি সংখ্যা=২ ৩: ৩=১+১+১=১+২=২+১ বিভক্তি সংখ্যা=৩ ৪: ৪=১+১+১+১=১+১+২=১+২+১=২+১+১=২+২ বিভক্তি সংখ্যা=৫ ৫: ৫=১+১+১+১+১=১+১+১+২=১+১+২+১=১+২+১+১=২+১+১+১ বিভক্তি সংখ্যা =৮=২+২+১=২+১+২=১+২+২ ধারাটি পরিচিত মনে হচ্ছে? অবশ্যই হবে। এ তো সেই বিরহাঙ্ক-ফিবুনাচি সংখ্যামালা। তাহলে ৬টি পটের ভেতর ৬টি ফুলের চারা বসাতে হলে (যাতে কোনোটিতে ১টি কি ২টির বেশি চারা থাকবে না) কত রকমভাবে সেটা সাজানো সম্ভব?

একটু ধৈর্য ধরে গুনতে থাকলে অনায়াসে পেয়ে যাবেন সেই সংখ্যাটি-১৩; ৮ এর পরে ঠিক যে সংখ্যাটি পাবার কথা বিরহাঙ্ক-ফিবুনাচি রাশিতে। তাহলে দেখা যাচ্ছে, প্রতি পটে ০, ১, বা ২ সংখ্যক চারা বসানোর নিয়ম অনুযায়ী ক-সংখ্যক পটে ক-সংখ্যক চারা লাগাতে হলে কতভাবে তা করা যেতে পারে সেটা বের করতে হলে উপরোক্ত রাশিটির দিকে তাকালেই হয়। সজাগ পাঠক এখানে প্রশ্ন তুলতে পারেন: ৬টি পটের জন্য আমাদের এত মাথা ঘামাতে হলো, ১০টা কি ৫০টা পট আর পঞ্চাশটা চারা লাগাতে হলে তো সর্বনাশ-সারা দিন সারা রাত লেগে যাবে এই গোনার কাজে, দুনিয়ার আর সব কাজ তখন ভেস্তে যাওয়ার অবস্থা হবে। হ্যাঁ, যথার্থ অভিযোগ। সে জন্যে গাণিতিক হিসাবে আমার একটা সোজা দাওয়াই যে নেই তা নয়। স্কুল-কলেজে পড়াকালে আপনি নিশ্চয়ই অঙ্কের বিন্যাস (Permutations) আর সমাহার (Combinations) বিষয় দুটো পড়েছিলেন। এ দুটোর ব্যবহার তো সম্ভাবনা শাস্ত্রে (Probability Theory) রীতিমতো অপরিহার্য। বীজগণিতেও তা-ই এবং এখানে যে ফুলের চারা আর পটবিন্যাসের কথা বললাম, এখানেও এ-দুটি বিষয় জানা থাকলে গুনতে খুব সুবিধা হয়। তাহলে ওপরের সংখ্যাগুলো আপনি চোখের পলকে বের করে ফেলতে পারতেন। এই সংখ্যাবিভক্তি, যার অন্যতম উদাহরণ থেকে বেরিয়ে এসেছে ফিবুনাচি-বিরহাঙ্ক সংখ্যামালা, তার প্রয়োগশীলতা আরও অনেক জায়গাতেই। পদার্থবিজ্ঞান আর রসায়নশাস্ত্র দুটিতেই ব্যবহৃত একটি শাখার নাম পরিসাংখ্যানিক বলবিদ্যা (Statistical Mechanics), যেখানে কোন ধরনের অণু কোন খোপে যাবে (খোপ বলতে কী বোঝায় সেটা একেক ক্ষেত্রে একেক রকম-কখনো ঘনত্ব, কখনো শক্তি, কখনো বা পরমাণুর বিশেষ ধর্মনির্ভর) এবং কতগুলো, সে অনুযায়ী একেক গণনাপদ্ধতি থেকে বেরিয়ে আসবে একেকটি সংখ্যা-ঠিক পার্টিশন তত্ত্বেরই মতো। কথাগুলো উল্লেখ করলাম এই জন্য যে, গণিতের বিমূর্ত রূপ অনেক সময় সাধারণ পাঠককে ভাবিয়ে তোলে বাস্তব জীবনে এসবের আদৌ কোনো প্রয়োজন আছে কি না।

আমার উপরোক্ত মন্তব্যগুলোতে আশা করি এটুকু বোঝাতে পারলাম যে, এই আপাতশুষ্ক, অর্থহীন সংখ্যামালা কেবল শ্বেতপ্রস্তরের অট্টালিকাবাসী অলস গাণিতিকদের সুখবিলাসের প্রমোদাগার নয়, এর একটা বাস্তব প্রয়োগশীলতাও আছে। গণিতের প্রকৃতিটাই এ রকম। দেখতে মনে হয় বাস্তবতার সঙ্গে এগুলোর কোনো সম্পর্ক নেই। গোড়াতে হয়তো প্রয়োগযোগ্যতার কথা ভেবেই তার আবিষ্কারক এটা নিয়ে আসেননি আমাদের কাছে। কিন্তু কালে কালে দেখা গেল ঠিক এই জিনিসটাই ভীষণ জটিল একটা সমস্যার সমাধান করে দিয়েছে সম্পূর্ণ ভিন্ন একটা ব্যবহারিক শাখায়।

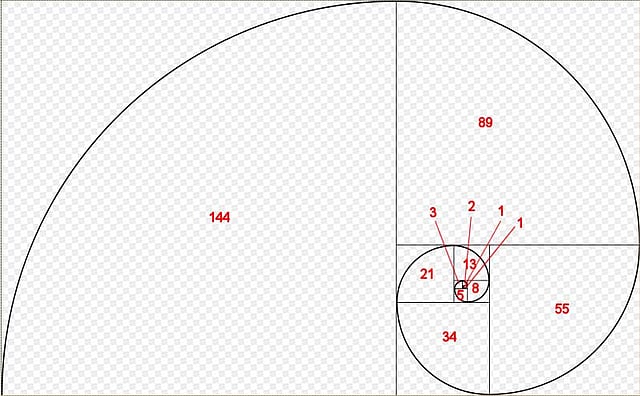
ফলিতবিজ্ঞান আর বিমূর্ত গণিতের মাঝে এ এক বিচিত্র সখা-সখীর সম্পর্ক। কখনো বিজ্ঞান নতুন পথের ইঙ্গিত দেয় গণিতকে, আবার গণিতই কখনো বিজ্ঞানকে হাত ধরে নিয়ে যায় সামনে। এ কারণেই লেওনার্দো দ্য ভিঞ্চি আর গ্যালিলিও গ্যালিলি, দুই মহাপুরুষ ঠিক একই কথা বলেছিলেন গণিত সম্বন্ধে, ‘গণিত হলো প্রকৃতির ভাষা।’ আমরা যারা মূলত গণিতের ছাত্র, তাদের কাছে ‘ফিবুনাচি’ সংখ্যা একটি অতিপরিচিত, অতিপ্রিয় ও বহুলব্যবহৃত সংখ্যা। আমরা ভাবতাম এমন একটা অসাধারণ জিনিস কেমন করে দ্বাদশ শতাব্দীতে ইতালিয়ান এক গাণিতিকের মাথায় ঢুকেছিল। অবাক হয়ে যেতাম লোকটার ধীশক্তির কথা চিন্তা করে। তারপর যখন জানলাম, না, এটা ভারতীয় পণ্ডিতরাই প্রথম আবিষ্কার করেছিলেন ফিবুনাচিরও ৬০০-৭০০ বছর আগে এবং অঙ্কের ভেতর দিয়ে নয়, কবিতার ভেতর দিয়ে, তখন বিস্ময়ে স্তম্ভিত হয়ে থাকা ছাড়া আর কী করার আছে বলুন। এখন আমার সন্দেহ হচ্ছে, হয়তো সংগীত আর নৃত্যশিল্পতেও ফিবুনাচি-বিরহাঙ্ককে পাওয়া যাবে, কারণ সেখানে তো প্রথম শিক্ষাটাই হলো কীভাবে গুনতে হয়। নৃত্যশিল্পের খবর আমি এখনো জানি না, তবে সংগীতে যে ফিবুনাচি-বিরহাঙ্ক আছে, তার প্রমাণ তো আমি নিজেই দেখেছি। পাঠকের সুবিধার জন্যে রাশিটিকে দ্বিতীয়বার লেখা যাক নিচে: ০, ১, ১, ২, ৩, ৫, ৮, ১৩, ২১, ৩৪, ৫৫, ৮৯, ১৪৪, ... সংখ্যাগুলো যে বেড়ে বেড়ে একেবারে সীমার বাইরে চলে যাচ্ছে, সেটা তো পরিষ্কার বোঝাই যাচ্ছে। তবে দেখা যাক এদের অনুপাতগুলো কীভাবে এগুচ্ছে। ২/১=২; ৩/২=১.৫; ৫/৩=১.৬৬৬; ৮/৫=১.৬০০; ১৩/৮=১.৬২৫; ২১/১৩=১.৬১৫; ৩৪/২১=১.৬১৯; ৫৫/৩৪=১.৬১৭; ... একটা প্যাটার্ন বেরিয়ে আসছে, তা-ই না? সংখ্যাটি ১.৬ এর কাছাকাছি ঘোরাঘুরি করছে, তাতে কোনো সন্দেহ নেই। আসলে গণিতের লোকেরা খুব সহজেই প্রমাণ করে দিয়েছেন যে চূড়ান্ত সীমায় গিয়ে সংখ্যাটি ১.৬১৮ এর খুব সন্নিকটে একবারে স্থির হয়ে বসে, যদিও দশমিক সংখ্যাগুলো কখনোই শেষ হয়ে যায় না। তার অর্থ সংখ্যাটি অমূলদ! তবে অমূলক নয়। এর একটা গভীর তাৎপর্য আছে। দেখা যায় যে সংখ্যাটি আসলে প্রকৃতিরই একটি গোপন কোডের মতো একটা সংকেত সংখ্যা। রহস্যটি সর্বপ্রথম উদ্ধার করেছিলেন গ্রিক দার্শনিক-গাণিতিক পাইথাগোরাস (খ্রিষ্ট-পূর্ব ৫৬৯-৫০০), অনেকটা ঘটনাক্রমে এবং তাঁর নিজেরই পরম অনিচ্ছাবশত। একটা একতারা বাদ্যযন্ত্র নিয়ে সুর তোলার খেলা খেলতে খেলতে হঠাৎ আবিষ্কার করে ফেললেন যে তারের যে জায়গাটিতে টোকা দিলে সবচেয়ে মধুর সুরটি বেরিয়ে আসে তার সঙ্গে এই সংখ্যাটির ওতপ্রোত সম্পর্ক।

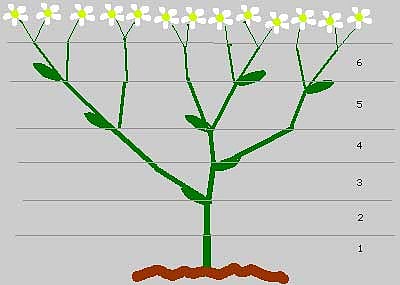
এটি অমূলদ সংখ্যা ঠিকই, কিন্তু সে সময়কার অমূলদবিরোধী চিন্তাধারার কথা ভেবে তিনি সেটা কারও কাছে ফাঁস করতে চাননি। যা-ই হোক, কালক্রমে রহস্যটা আর গোপন থাকে না এবং তার একটি শিরোনামও তৈরি হয়ে যায়: সুবর্ণ অনুপাত (The Golden Ratio)। অনেকের ধারণা, এই সুবর্ণ সংখ্যাটি শিল্পকলার একাধিক শাখায় আত্মপ্রকাশ করে শিল্পীর অজান্তেই। অঙ্কন-শিল্পের কর্মীরা যখন জ্যামিতিক অনুপাত ব্যবহার করেন তাঁদের কাজে, তখন দেখা যায় যে এই অনুপাতটিই তাঁদের ভাব প্রকাশের জন্য সবচেয়ে উপযোগী সংখ্যা। স্থাপত্যশিল্পেরও নাকি একই ধারা-অন্তত তা-ই শোনা যায় অনেকের মুখে, যদিও সেটা একেবারে অবিতর্কিত নয়। ফিবুনাচির সঙ্গে বিরহাঙ্কের সম্পর্ক বিষয়ে ইন্টারনেট ঘেঁটে আমি আবিষ্কার করলাম যে ব্যাপারটি পশ্চিমা জগতে এখন খুব অজানা কিছু নয়। পিটার ক্যামেরন বলে এক ভদ্রলোক তাঁর ব্যক্তিগত ব্লগে ফিবুনাচি রাশির ওপর ধারাবাহিকভাবে বেশ কটি লেখা প্রকাশ করেছেন (cameroncounts.wordpress.com/2012/06-18fibonacci-numbers-I/) । এতে তিনি বিরহাঙ্ক পণ্ডিতের কথা সসম্মানে উল্লেখ করেছেন এবং পাশ্চাত্য পাঠকদের কাছে সেটা উপস্থাপন করার চেষ্টা করেছেন। সে সুযোগে বিরহাঙ্ক রাশির সঙ্গে সামঞ্জস্যপূর্ণ একটা মডেল তিনি নিজে থেকেই তৈরি করে নিয়েছেন, যা সাধারণ পাঠকদের কাছে বেশ সহজবোধ্য হওয়া উচিত। ধরুন আপনি একটা দোতলা বাড়ির একতলার সিঁড়িতে দাঁড়িয়ে আছেন, দোতলায় ওঠার বাসনায়। ধরা যাক, একেক ধাপে আপনি হয় একটা সিঁড়ি বা দুটো সিঁড়ি উঠতে পারবেন, তার বেশি নয়। তাহলে মোট ক-সংখ্যক সিঁড়ি অতিক্রম করতে হলে আপনি কতভাবে তা পারবেন? সিঁড়ির সংখ্যা যদি ১ হয়, তাহলে স্পষ্টতই ১ উপায়ে। ২ হলে ২ ভাবে (হয় ১, ১ করে বা একবারেই ২), ৩ হলে ১,১,১; ১;২; ২,১ অর্থাৎ ৩ উপায়ে। সিঁড়ি সংখ্যা যদি ৪ হয় তাহলে ১,১,১,১; ১,২,২; ২,১,১; ১,২,১; ২,২-মোট ৫ উপায়ে। পরিষ্কার দেখা যাচ্ছে সেই আগের সংখ্যাগুলি। ক-সংখ্যাক সিঁড়ি অতিক্রম করতে হলে ঠিক কতভাবে তা করা যেতে পারে, তার একটা গাণিতিক সূত্র আছে। সেটা না হয় না-ই উল্লেখ করলাম। এমনিতেই আমার অগাণিতিক পাঠকেরা হয়তো একটু ক্লান্ত হয়ে পড়েছেন। পরের অধ্যায়গুলোতে আমি ফিবুনাচি আর বিরহাঙ্ক বাবুর সঙ্গ নিয়ে প্রকৃতির এক গোপন রহস্যপুরিতে চলে যাব। শম্বুকশাবকের ক্রমবৃদ্ধি শৈশব থেকে প্রাপ্তবয়সে পৌঁছানোর প্রক্রিয়াটি সম্বন্ধে আমাদের সবারই একটা মোটামুটি ধারণা আছে, যদিও সে ধারণার সঙ্গে বিশেষজ্ঞ জ্ঞানের কোনো তুলনাই হয় না। কিন্তু কেউ কি কখনো ভেবে দেখেছেন সমুদ্র উপকূলে এই যে এত এত শামুক চোখে পড়ে আমাদের এবং দেখার পর নানাবিধ রোমান্টিক ভাবনাতে নিমগ্ন হয়ে পড়ি মাঝে মাঝে, তারা আসলে কীভাবে ক্ষুদ্র কণার মতো অস্তিত্ব নিয়ে জন্মানোর পর আস্তে আস্তে পূর্ণাঙ্গ শম্বুকে পরিণত হয়? সঠিক প্রক্রিয়াটি হয়তো শামুকবিশারদ প্রাণিবিজ্ঞানী ছাড়া আর কেউ পুরোপুরি বলতে পারবেন না। তবে মূল ঘটনাটি অনেকটা এরকম: শুরুতে তার ছোট্ট ১+১ মাপের কামরা। আস্তে আস্তে বাড়তে থাকলে আরেকটা ঘরের দরকার হয়ে পড়ে। কিন্তু নতুন জায়গাতে নতুন কোনো ঘর তৈরি করার সামর্থ্য নেই বলে সে আগের ঘরের দেয়াল ধরেই ঠিক একই মাপের আরেকটা ঘর তৈরি করে নেয়। পরের দফাতে প্রথম আর দ্বিতীয় দফার মাপ যোগ করে যা পাওয়া যায়, অর্থাৎ ৩, তাই দিয়ে সন্তুষ্ট থাকতে হয়। তারও পরেরটিতে সেই একই ফর্মুলা ব্যবহার করে সে পায় ৫ মাপের ঘর। এভাবে যেতে যেতে পূর্ণাঙ্গ দেহে পৌঁছাতে তাকে নির্মাণ করতে হয় একটি ফিবুনাচি-বিরহাঙ্ক মাপের গৃহ: ১, ২, ৩, ৫, ৮, ১৩, ২১, ৩৪, ৫৫, ৮৯, ১৪৪, ...। শেষমেশ তার বাড়িটা নেহাত মন্দ দেখায় না, কি বলেন? প্রতিসাম্য আছে এর গঠনে। গণিতের ভাষায় একে বলা হয় Outward Spiral বা বহির্মুখী চক্র। এবার একটি উদাহরণ দেব। প্রকৃতির কাছ থেকেই ধার করা। যাতে বহির্মুখী ও অন্তর্মুখী, উভয় প্রকারের চক্র পাওয়া যাবে একই জিনিসের ভেতর: সূর্যমুখী ফুল! ফুল আমরা সবাই ভালোবাসি। কিন্তু কেউ কি কখনো খেয়াল করে দেখেছেন কোন ফুলের পাপড়িসংখ্যা কত। উদ্ভিদবিদদের গণনা অনুযায়ী মেরিগোল্ড বা গাঁদাফুলের পাপড়িসংখ্যা ১৩, এস্টারফুলের পাপড়ি ২১, কোনো কোনো ডেইজির ৩৪, বেশির ভাগেরই ৫৫ বা ৮৯। ফুলের চাষাবাদ করে যারা জীবিকা নির্বাহ করেন তারা অনেক সময় কৃত্রিম উপায়ে পাপড়ির সংখ্যা বাড়িয়ে দ্বিগুণ করে তোলেন। সাধারণত ডেইজি ফুলের পাপড়িসংখ্যা ৩৭ বা ৩৩ এমন দৃশ্য খুবই বিরল। যদি হয় সেটা নেহাতই ব্যতিক্রম। সূর্যমুখীটার দিকে খুব মনোযোগ দিয়ে তাকালে বোঝা যাবে দুটি পরিষ্কার ধারা। একটি অন্তর্মুখী। আরেকটি বহির্মুখী চক্র বেরিয়ে এসেছে এর ভেতর থেকে। অনেকটা বাইসাইকেলের চাকার মতো। ধৈর্য ধরে, বীক্ষণযন্ত্রের সাহায্য নিয়ে যদি দেখেন, তাহলে হয়তো একটা পরিণত ডেইজি পরিবারের অন্তর্গত সূর্যমুখীর একদিকের পাপড়িসংখ্যা ২১ হলে আরেকদিকে হবে ৩৪; একদিকে ৫৫ হলে আরেকদিকে হবে ৮৯, ...। প্রথম থেকে প্রাপ্ত অবস্থা অবধি ঠিক কী নিয়মে তারা ক্রমে ক্রমে ছড়িয়ে পড়ে তার একটা জ্যামিতিক আভাস দেওয়া হলো নিচে। প্রথমে ১, তারপর ২, পরে ৩, তারপর ৫, ৮, ১৩, ২১, ৩৪, ৫৫, ৮৯, ..., অর্থাৎ ঠিক ফিবুনাচি-বিরহাঙ্ককে অনুসরণ করে। এখানে বলে রাখা ভালো যে, চক্র দুটিকে বহির্মুখী আর অন্তর্মুখী না বলে ঘড়ির কাঁটার বিপরীত (Anticlockwise or Positive) বা সমদিকও (Clockwise or Negative) বলা যেতে পারত। বাংলাতে এদের ধনাত্মক আর ঋণাত্মক দিকও বলা যায়। পদার্থবিজ্ঞানে, বিশেষ করে আধুনিক আণবিক-পরমাণবিক বিজ্ঞানে, এই দুটি দিকের পার্থক্য খুবই মৌলিক একটি বিষয়। যা-ই হোক, উদ্ভিদজগতের এই তথ্য আমি সংগ্রহ করেছি The Mathematics of Life, by Ian Stewart, Published in the United States by Basic Books, in 2011, সূত্রটি থেকে। বাস্তব জীবনে গণিতের স্থান কোথায়, সে বিষয়ে অনেকেরই প্রচুর কৌতূহল, সেটা বোধ হয় অত্যুক্তি নয়। এ বইটিতে পাঠক আরও দেখতে পাবেন ফিবুনাচি-বিরহাঙ্ক রাশিটি কী আশ্চর্য উপায়ে একটি আনারসের গায়ের ওপর আঁকা (আক্ষরিক অর্থে নয় যদিও) রয়েছে। আমার শেষ উদাহরণ হবে একটা গাছ কীভাবে চারা থেকে ধীরে ধীরে বড় হতে থাকে। সব রকম গাছ হয়তো নয়, ফিবুনাচি-বিরহাঙ্কের আওতায়, তবে কোনো কোনো গাছ অবশ্যই। বিশেষ করে বিলেতে একটা ফুল আছে যার নাম Sneezewort বা Sneezeweed (যার আক্ষরিক বাংলা করলে দাঁড়ায় হাঁচিগাছ বা হাঁচিগুল্ম)। এ গাছের ফুলগুলোর পাপড়ি সাদা, তবে মাঝখানের কোষটুকু সবুজ বা বাদামি রঙের, আকারে বেশ ছোটই বলা চলে, দেখতে অনেকটা বোতামের মতো। চারা থেকে আস্তে আস্তে বেড়ে ওঠার নিয়মটা খানিক এরকম: প্রথম যখন একটা কুঁড়ি গজায়, সে কুঁড়ি থেকে নতুন কুঁড়ি বেরুতে সাধারণত মাস দুয়েক সময় লাগে (আনুমানিক)। তখন তার গায়ে যথেষ্ট শক্তি এসে যায় শাখাপ্রশাখার ভার বহন করবার। তাহলে যদি ধরা হয় যে প্রতি মাসের শেষে নতুন শাখা গজাতে শুরু করে, দেখা যাবে ৫-৬ মাস পরে গাছটা শাখা-প্রশাখায় বিস্তৃত হয়ে এই প্রতিবেদনের সঙ্গে প্রকাশিত ছবিটার মতো দাঁড়িয়ে গেছে। এবার একটু মনোযোগ দিয়ে গুনে দেখুন, ফিবুনাচি-বিরহাঙ্ককে খুঁজে পান কি না। প্রথম মাসে ১টি, দ্বিতীয় মাসে ১টি, তৃতীয় মাসে ২টি, চতুর্থ মাসে ৩টি, পঞ্চম মাসে ৫টি, ... ঠিক যেভাবে শামুকের শরীর বাড়ে, ডেইজিফুলের পাপড়ি ছড়ায় এবং সংস্কৃত-প্রাকৃত কবিতার ছন্দবিন্যাস করা হয়। বিরহাঙ্ক বা ফিবুনাচি, তাঁরা কি কেউ কল্পনা করেছিলেন যে তাঁদের এই খেলাচ্ছলে আবিষ্কার করা সংখ্যামালার মধ্যে আত গোপন করে ছিল প্রকৃতির প্রজননসূত্রের এক গূঢ়, গুপ্ত, রহস্য?

মীজান রহমান

অটোয়া, কানাডা
(এই লেখাটি ২০১৩ সালের এপ্রিলে লেখা)